As we have seen in previous posts, it is essential to use alternative formulas, either time-weighted or money-weighted when there are situations of inflows or outflows in a portfolio, in order to properly calculate the return. This time we are going to show you how to calculate returns of a time-weighted portfolio, with some examples included.
Table of contents
ToggleFormula for calculating time-weighted portfolio returns
The most appropriate formula to compare the return between two assets or two portfolios, and the most commonly used, is the Time-Weighted Return (TWR) formula. This is the formula we use (by default) at inbestMe to calculate the return of our clients’ portfolios.
The formula is, (using the acronym TWR):
(F1):
TWR = [(1+PRN) x (1+ PRN) x … – 1] x 100
Being:
(F2): PRN= ((NAVF-CF)/NAVI ) -1
Or, in other words: PRN= (NAVF-NAVI-CF)/NAVI
And being:
| PRN | Profitability Ratio for the period N |
| NAVF | Nav or final value of the portfolio for the period |
| NAVI | Nav or initial value of the portfolio for the period |
| CF | Cash Flow (cash inflows or outflows in the portfolio) |
Therefore, for each period where we have inflows or outflows of money we will need to calculate the PRN, and for this we will need to have the NAVI (initial value of the portfolio) NAVF (final value of the portfolio) and the movement of money (positive or negative at the end of that period).
In the event that the portfolio is made up of several funds or securities, we must simply add the final value of all the assets that make up the portfolio.
We will have to calculate as many PRN (using F2) as periods where there is a CF (cash flow +/-). We will calculate the PRN of each period where this occurs, and finally we will make an arithmetic progression with all the PRN according to F1.
Finally, we subtract 1 and multiply by 100 to express it as a percentage.
In this way, we will obtain the accumulated value of the portfolio.
To convert it into an APY, we must apply the formula:
(1+TWR)^(1/years)-1
Examples of how to calculate the TWR of a portfolio
Example 1
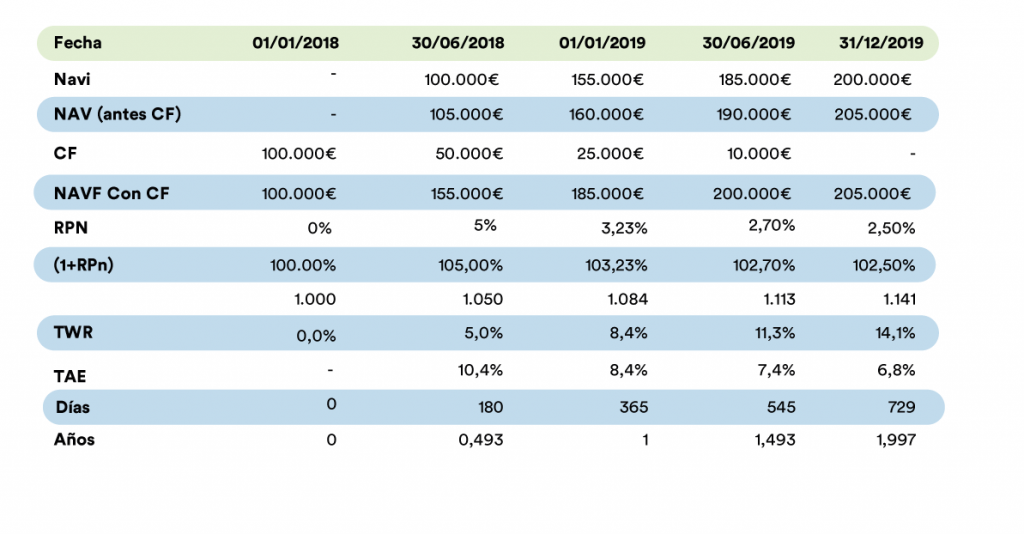
In the table above we see how to calculate the TWR and the APY for a portfolio starting with 100,000 and where there are 3 contributions of 50,000, 25,000 and 10,000 respectively.
The final calculation is made without additional input (this is compatible with the formula by setting CF=0) and we also calculate the TWRs and APYs for the different periods.
As of 12/31/2019, the TWR is 14.1% and the APY is 6.8%.
Example 2
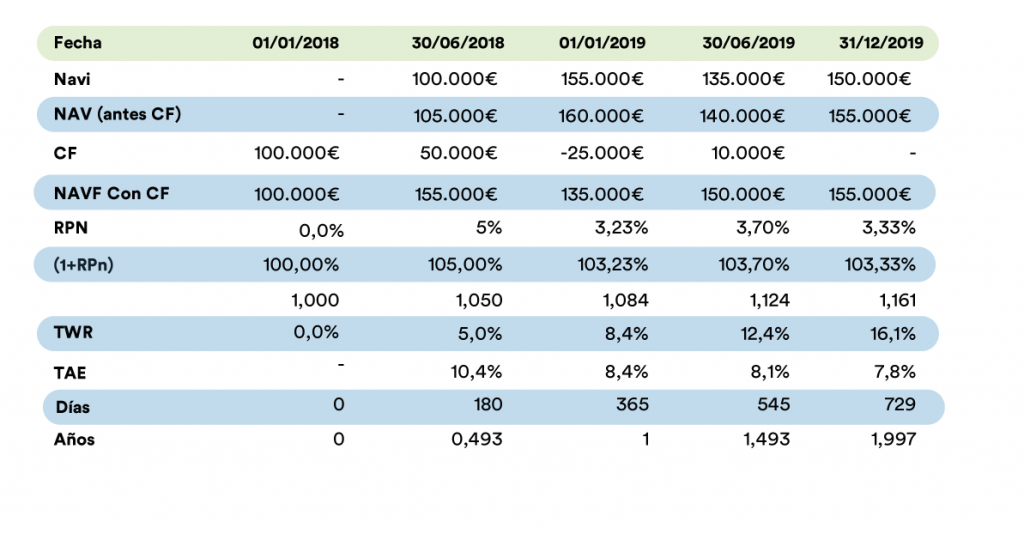
Example 2 is very similar to the previous one. But in this case we show how the formula works the same in the case of a withdrawal (1/1/2019).
As of 12/31/2019, the TWR is 16.1% and the APY is 7.8%.
Remember that NAVI and NAVF are simply the net asset values of the funds or stocks that make up the portfolio at the time of observation. It is normal to make the calculation after commissions, i.e., subtracting from the net asset value all the commissions that the portfolio has to bear (management, trading if any, and depository).
We can decide to make two calculations, before commissions or gross return before commissions and after commissions, which would be the net return after subtracting commissions. The latter is the one we calculate by default for our clients and for our model portfolios when we publish them.
Appendix: more details on the formulas
The PRN calculation formula can be adjusted depending on whether the cash flows are made at the beginning or at the end of the period. In the examples, we have considered that these occurred at the end of the period (we also find it easier to explain in this way).
If the inflows occur at the beginning of the period, the formula to be used is:
- PRN= (NAVF-NAVI-CF)/(NAVI+CF)
In fact, this is the formula used by Interactive Brokers (even for daily calculations) and therefore we also use it at inbestMe to be consistent. This calculation may give small differences, but in our experience they are minimal in daily calculations (what we do for our clients on their accounts). If you want to learn more about this topic in this article (Wikipedia) we think it covers all the details very well.










