Segons hem vist en posts anteriors és imprescindible usar fórmules alternatives sigui ponderant pel temps o ponderant pels diners quan es produeixen situacions d’entrades o retirades de diners en una cartera per a tenir el càlcul adequat de la rendibilitat.
Aquesta vegada vam mostrar com calcular la rendibilitat d’una cartera ponderant pels diners incloent un exemple.
Fórmula per a calcular la rendibilitat d’una cartera ponderada pels diners
La fórmula alternativa al TWR (rendibilitat ponderada pel temps) consisteix a ponderar pels diners. En anglès s’utilitzen les sigles MWR (Money Weighted Return) per a referir-se a aquesta fórmula.
Encara que la fórmula més usada (per defecte en inbestMe) és el TWR, alternativament i de manera complementària pot ser útil calcular la rendibilitat de la nostra cartera ponderant pels diners. El MWR és útil per a determinar si hem estat bons triant el timing de les nostres inversions.
En realitat, per la concepció, té en compte la dimensió de les aportacions/retirades i el moment de la inversió, per això pren el nom de ponderada pels diners.
En inbestMe preferim no estar pendents del timing ni la profunditat de les nostres inversions. Recomanem programar tant com sigui possible el nostre estalvi/inversió de manera periòdica i automatitzada.
El MWR es calcula buscant la taxa de rendiment que igualarà els valors actuals de tots els fluxos de diners al valor de la inversió inicial.
Els coneixedors de la matemàtica financera veuran que aquesta definició en definitiva consisteix i és equivalent a calcular la TIR o valor present d’una inversió amb diferents fluxos d’entrada/sortida en el temps.
En aquest cas s’utilitza la versió alternativa a la TIR fent el càlcul del valor present buscant el valor present de les entrades/sortides igual a 0. Tinguem en compte que per definició la TIR és un valor anualitzat.
Una vegada obtingut haurem de convertir-ho en una rendibilitat acumulada amb una altra fórmula.
La fórmula del càlcul del TWR és (usant les sigles en anglès TWR i valor anualitzat):
(F1): VP = 0 = CF0 + CF1/(1+TWR)^1 + CF2/(1+TWR)^2 + … CFn/(1+TWR)^n
On CF0 és el primer valor dipositat a l’inici de la inversió i CF1, CF2. CFn són els diferents dipòsits (o retirades) en diferents moments de la història de la cartera. En el moment del càlcul haurem de considerar el valor final de la cartera com un flux de caixa més per a fer el càlcul.
Càlcul del TWR (valor acumulat):
(F2): (1+TWR)^(n)-1
Exemple de com calcular el MWR d’una cartera:
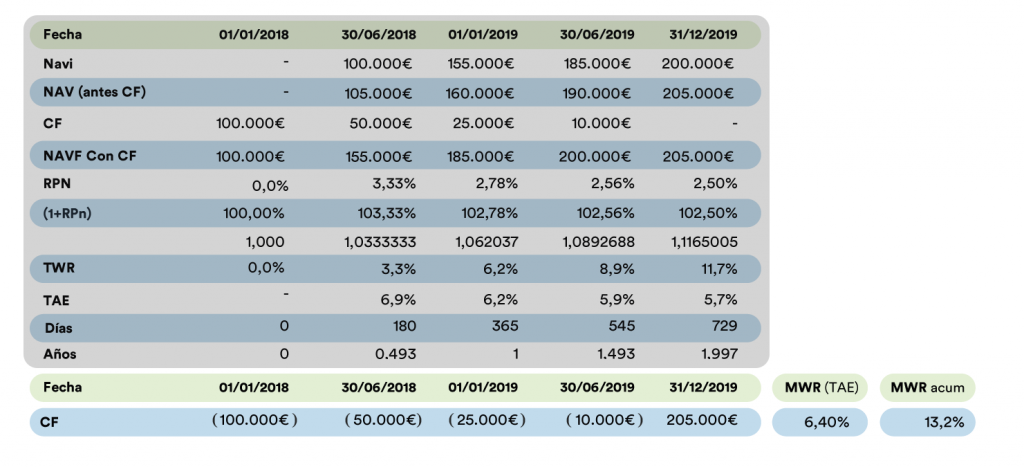
En la taula superior veiem com calcular el MWR (anualitzat primer, és a dir, la TAE) i el valor acumulat (MWR acumulat) per a una cartera que comença amb 100.000 euros i on hi ha 3 aportacions de 50.000, 25.000 i 10.000 respectivament.
En la taula de més amunt usem el mateix exemple que per al TWR. Hem ombrejat el càlcul del TWR i afegit dues files més per a veure com podem extreure la informació necessària de la mateixa taula: per a calcular el MWR només necessitem les dates i els imports de les entrades i sortides de diners.
Per a fer el càlcul haurem d’usar un Excel amb la fórmula especial de la TIR (IRR en anglès), TIR.NO.PER (XIRR en anglès) especialment dissenyada per a fluxs de caixa no regulars (aplicable a una cartera). Veiem a continuació com en Excel hem de seleccionar els valors, d’una banda, i les dates, d’altra banda.

En el nostre cas hem usat la fórmula en anglès. Si el nostre Excel està en castellà només s’ha de substituir XIRR per TIR.NO.PER.
Veiem com el resultat és:

Per a calcular el valor acumulat sol hem d’aplicar la fórmula que vam veure anteriorment, amb els números d’aquest exemple:
(1+0.0640)^1,997 – 1 = 13,2%
El període transcorregut des de la primera inversió fins a la data de càlcul (en l’exemple: 1,997 que podem observar al final de la taula de l’exemple a la dreta en la part ombrejada).
Comparació entre TWR i MWR
Si comparem aquest resultat amb el qual vam fer del TWR veurem que en aquest cas el valor resultant acumulat és una mica inferior amb la fórmula del MWR (13,2% vs. 14,1%) i que també es trasllada òbviament en una TAE una mica inferior (6,4% vs. 6,8%).
Aquest MWR més baix mostraria que l’inversor no ha encertat o no ha tingut sort amb el timing de la seva inversió.
D’altra banda, en general, el TWR mesura millor l’encert del gestor, per això s’usa més i és el càlcul que usem per defecte en inbestMe. De totes maneres és bo conèixer també la fórmula del MWR, ja que en casos extrems el TWR pot donar una informació poc rellevant per a l’inversor.
És important que l’inversor conegui aquests càlculs i el perquè del seu ús, ja que per defecte tenim la tendència a simplificar i usar l’interès simple (fórmula que no és vàlida quan hi ha entrades i sortides de capital).
Nota: el més correcte és fer aquests càlculs després de tots els costos que suporta la cartera (de gestió, trading si n’hi hagués i dipositària). Així ho fem en inbestMe per defecte per a les carteres dels nostres clients i per al càlcul de rendibilitat de les nostres carteres model. Evidentment, sempre podem decidir fer el càlcul després i abans de costos, deduint o no aquests mateixos del valor liquidatiu de la nostra cartera.