En anteriores posts hemos visto las diferentes formas de calcular la rentabilidad.
En este post veremos en la práctica el efecto que producen diferentes situaciones en el cálculo de la rentabilidad, en función de las diferentes fórmulas de cálculo. A través de los ejemplos veremos que los flujos adicionales de dinero son los que provocan la principal distorsión en los cálculos y cuál es la mejor fórmula para evitar esta distorsión.
Índice de contenido
ToggleRentabilidad lineal en los periodos sin flujos de caja adicionales
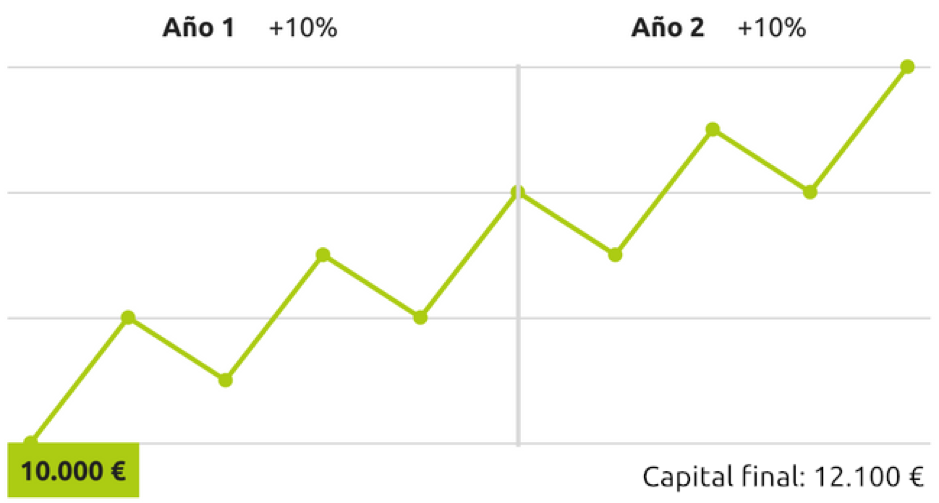
Ya hemos visto en otros posts que este caso es el único que no da problemas en los cálculos. Es decir, en todas las fórmulas las rentabilidades obtenidas son iguales:
Cálculo simple de la rentabilidad: 21% (12.100/10.000)-1
Rentabilidad ponderada por el tiempo: 21% ((1+0.10)*(1+0.10))-1
Rentabilidad ponderada por el dinero: 21% 12.100= (10.000*(1+i)^2
i=10%
(1+0.10)^2-1=21%
Lo que ocurre es que normalmente la realidad de la vida de una cartera de inversión pasa por situaciones más complejas. Normalmente hay aportaciones o salidas de capital en el tiempo y las rentabilidades son irregulares.
Veamos otros casos:
Rentabilidad lineal en los periodos, pero con flujo de caja adicional
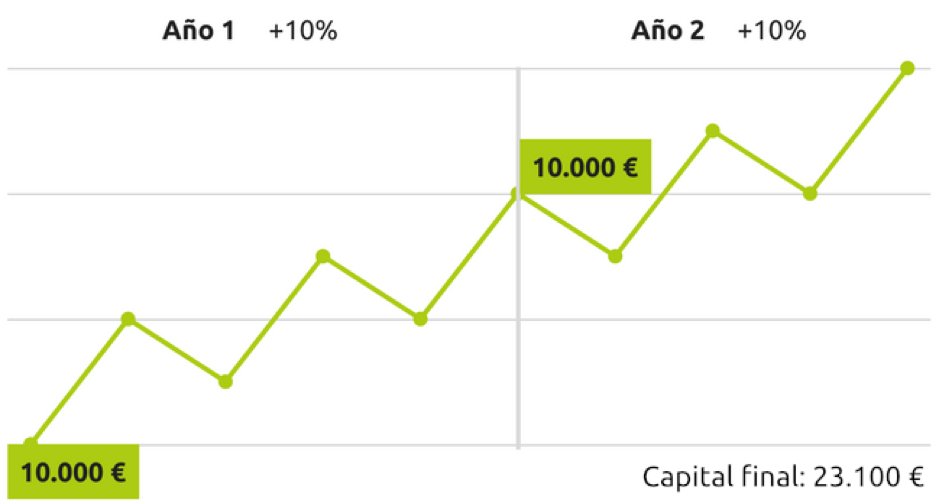
Cálculo simple de la rentabilidad: 15,5% 23.100/21.000-1
Rentabilidad ponderada por el tiempo: 21% ((1+0.10)*(1+0.10))-1
Rentabilidad ponderada por el dinero: 21% 12.100= (10.000*(1+i)^2)+(10.000*(1+i)^1
i=10%
(1+0.10)^2-1=21%
Sin embargo, el cálculo de la rentabilidad simple ya nos da una visión distorsionada.
Rentabilidad positiva diferente en los periodos sin flujos de caja
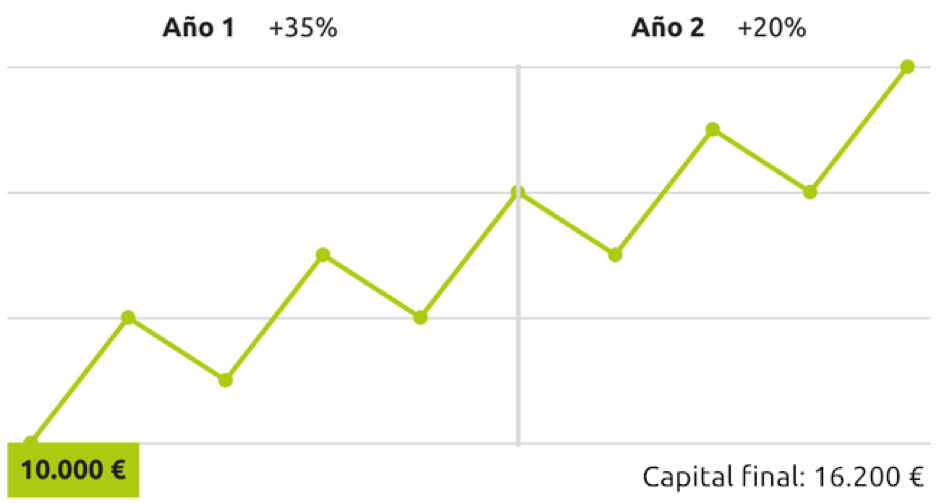
Las diferentes rentabilidades parciales en los sub periodos no provocan diferencia en el cálculo de la rentabilidad:
Cálculo simple de la rentabilidad: 62% 16.200/10.000-1
Rentabilidad ponderada por el tiempo: 62% ((1+0.35)*(1+0.20))-1
Rentabilidad ponderada por el dinero: 62% 16.200= 10.000*(1+i)^2
i=27.28%
(1+0.2728)^2-1=62%
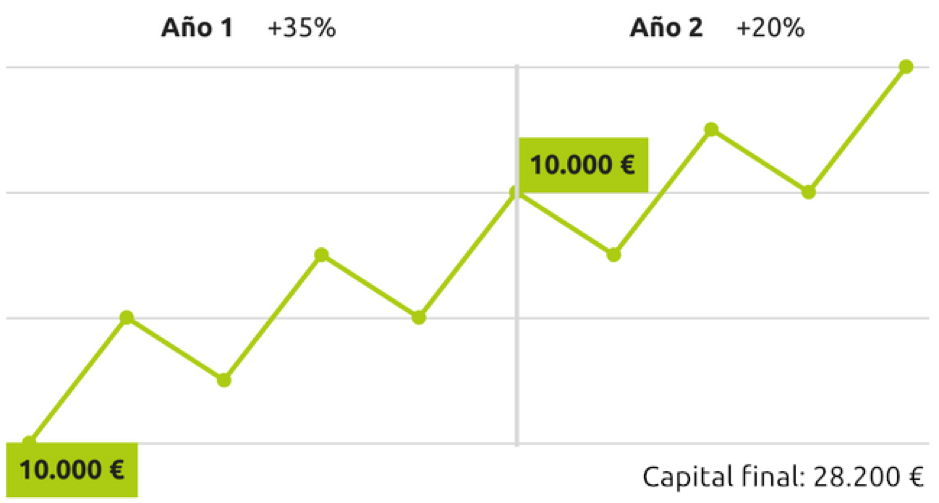
Rentabilidad positiva diferente en los periodos con flujo de caja
Como vemos en este caso, el flujo de caja adicional provoca de nuevo diferencias significativas en el cálculo de rentabilidades:
Cálculo simple de la rentabilidad: 41% (28.200/20.000)-1
Rentabilidad ponderada por el tiempo: 62% (( 1 + 0.35 ) * ( 1 + 0.20 ) ) – 1
Rentabilidad ponderada por el dinero: 56,8% 28.200 = (10.000 * (1 + i) ^2) + 10.000 * (1 + i ) ^1 )
i = 25.2%
( 1 + 0.252 ) ^2 – 1 = 56.8%
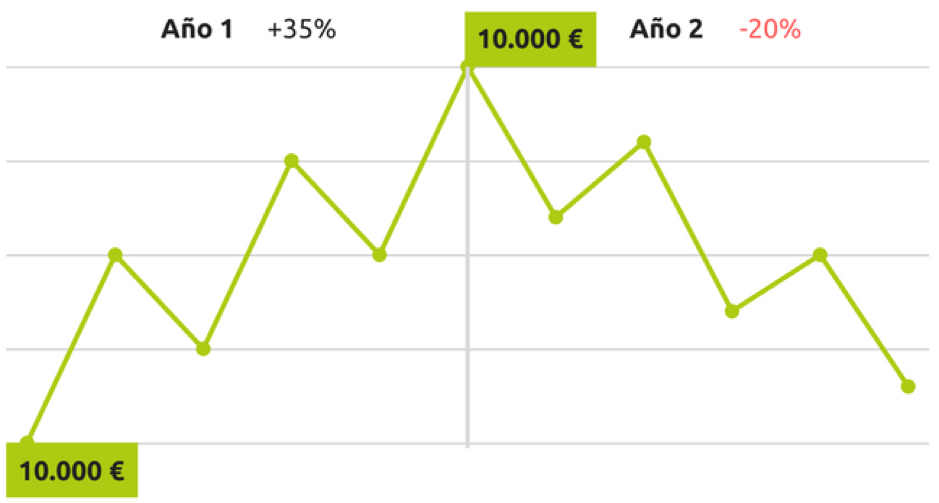
Rentabilidad positiva el primer año, negativa el segundo con flujo de caja
Este es posiblemente el caso más difícil de entender. La sensación para el inversor es de estar perdiendo dinero ya que su valor final es inferior a la inversión realizada. En este caso el cliente ha aportado 20,000€. Esto queda reflejado tanto en el cálculo de la rentabilidad simple como en la ponderada por el dinero. Pero no es así en la rentabilidad ponderada por el tiempo, que es positiva. Puede ser de ayuda el pensar que la combinación de un año bueno del +35% con un año malo de un -20%, tiene que dar como resultado una rentabilidad positiva. Una indicación de ello es que el promedio aritmético, (aun no siendo una medida válida si es indicativa) daría 7,5%, cercano al 8% que nos refleja la rentabilidad ponderada por el tiempo.
Cálculo simple de la rentabilidad: -6% 18.800/10.000 -1
Rentabilidad ponderada por el tiempo: +8% (( 1 + 0.35 ) * ( 1 – 0.20 ) ) – 1 = 8.0%
Rentabilidad ponderada por el dinero: -7,9% 18.800 = ( 10.000 * ( 1 + i ) ^2 ) + ( 10.000 * ( 1 + i ) ^1 )
i = -4.1%
( 1 – 0.041 ) ^2 – 1 = -7.9%
Es por esta razón que la rentabilidad ponderada por el tiempo es la fórmula utilizada por la industria financiera ya que es la que refleja mejor el impacto real en la rentabilidad de la gestión de una cartera y permite comparar entre activos. También es el cálculo utilizado por omisión por inbestMe.
Te recomendamos leer estos dos artículos adicionalmente para entender más sobre este tema:
Las múltiples caras de la rentabilidad I
Las múltiples caras de la rentabilidad II
[