La desviación estándar es una medida estadística que mide cuánto se dispersan los valores en torno a su promedio.
¿Por qué dedicar una publicación a una medida estadística? Porque en el contexto de la teoría de la cartera moderna, la desviación estándar se ha convertido en sinónimo de riesgo. Un activo cuya rentabilidad tiene una desviación estándar más alta es más volátil, y se considera más arriesgado que un activo con una volatilidad más baja.
Dado que el mercado generalmente ofrece una remuneración según el riesgo soportado, una mayor volatilidad se traduce en un mayor rendimiento esperado.
Índice de contenido
ToggleLa desviación estándar como medida de la incertidumbre
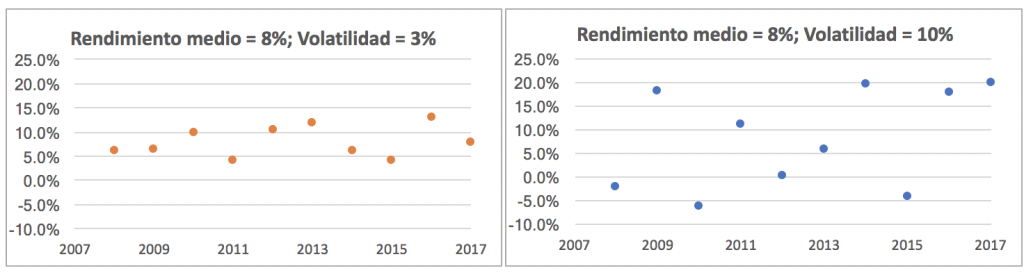
Si se asumen dos inversiones diferentes, con la misma rentabilidad esperada pero con diferente volatilidad, la que tenga mayor volatilidad presentará rendimientos mucho más dispersos respecto a la media. En el gráfico de más abajo comparamos por ejemplo una misma rentabilidad del 8% con diferente volatilidad del 3% y del 10%:
Por lo tanto, la volatilidad representa una medida de la incertidumbre relacionada con la obtención de un rendimiento igual al rendimiento esperado. Si la volatilidad es baja, los rendimientos no difieren mucho de la rentabilidad media, si la volatilidad es alta, los rendimientos son mucho más dispersos.
¿Cómo se calcula la desviación estándar?
Para calcular el valor de la desviación estándar σ debemos:
- Calcular la media de la rentabilidad (μ)
- Obtener la desviación de cada rentabilidad de la media (ri– μ)
- Elevar al cuadrado las desviaciones para obtener todos los valores positivos (ri– μ)2
- Sumar todas las altas desviaciones elevadas al cuadrado ∑(ri– μ)2
- Hacer la media de las desviaciones cuadradas Σ (ri – μ) 2 / N. Esta cantidad se llama varianza. Si es una muestra, el denominador se convierte en (n-1) en lugar de N
- Calcular la raíz cuadrada del resultado para obtener la desviación estándar
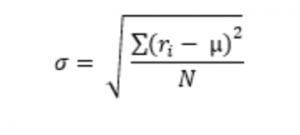

De una forma menos tediosa, puedes usar la función de EXCEL STDV.P (o EXCEL STDV.C si se considera una muestra, las funciones expresadas en inglés). Calculamos la desviación estándar de cuatro números (3, 5, 8 y 12) a través de todos los pasos enumerados anteriormente y de la manera más breve utilizando la función de Excel para verificar que los resultados coinciden en la siguiente tabla:
Lo que se obtiene es una medida de la dispersión de los rendimientos en torno a su media. Cuanto mayor es la desviación estándar, mayor es la dispersión y viceversa. Como ya se mencionó, la desviación estándar en finanzas se usa como una medida de volatilidad y a su vez la volatilidad es la medida del riesgo más usada.
Desviación estándar y distribución normal
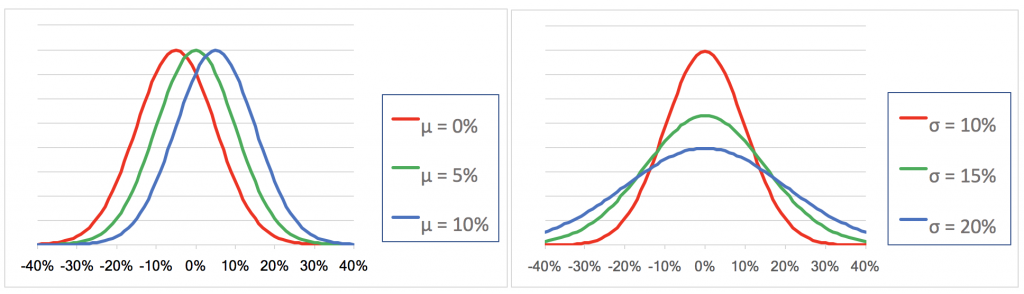
En general, se supone que los rendimientos de una inversión se distribuyen de manera normal. La distribución normal es aquella cuya función de densidad de probabilidad toma la forma clásica de campana. La distribución normal se debe describir con solo dos parámetros: la media (que define el valor central) y la desviación estándar (que describe el ancho de la campana).
La media μ define la ubicación de la distribución. La desviación estándar σ define su ancho. A medida que el promedio varía, el centro de la distribución se mueve a lo largo del eje horizontal mientras que la forma cambia de acuerdo con la variación de la desviación estándar. La curva se aplana con una volatilidad creciente mientras se vuelve más delgada y más alta a medida que disminuye la volatilidad.
Desviación estándar y probabilidad de un evento
En una distribución normal, la probabilidad de que la variable tome un cierto valor puede estar relacionada con la distancia respecto a la media en términos de desviaciones estándar. Intuitivamente, los valores muy distantes de la media se repiten con menos frecuencia, mientras que los valores cercanos al promedio son más comunes
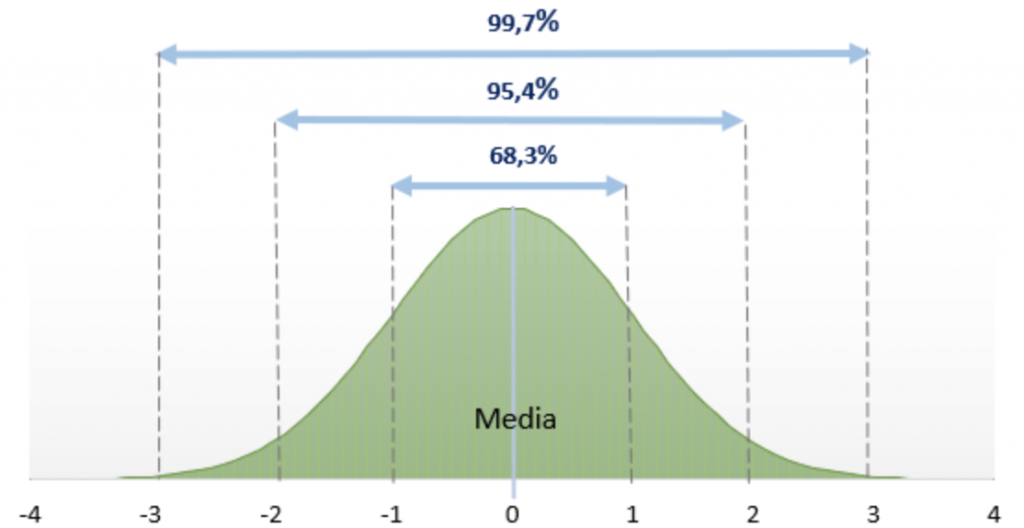
Una propiedad importante de una distribución normal es que podemos esperar que:
- el 68.3% de los valores se distribuyen dentro de una desviación estándar de la media,
- el 95.4% dentro de dos desviaciones estándar de la media,
- el 99.7% dentro de 3 desviaciones estándar del promedio.
Por lo tanto, dado un rendimiento y volatilidad esperados, se pueden definir intervalos dentro de los cuales debería caer un cierto porcentaje de rentabilidad. Lo que es importante reiterar es que, sea cual sea el valor asumido por la media y la desviación estándar de la distribución, el área bajo la curva entre la media y n las desviaciones estándar sigue siendo la misma. Cualquiera que sea el centro y la forma de la curva, el área entre +1 y -1 desviación estándar siempre contendrá el 68.3% de los valores.
En el caso de una inversión con un rendimiento esperado del 10% y una desviación estándar σ del 15%, podemos esperar que el 68.3% de los rendimientos realmente obtenidos estén entre -5% (10% -15%) y 25% ( 10% + 15%), ese 95.4% está entre -20% (10% -2 * 15%) y 40% (10% + 2 * 15%) y ese 99.7% está entre -35% ( 10% -3 * 15%) y 55% (10% + 3 * 15%).
Si conocemos la media y la desviación estándar de la distribución de los retornos y asumimos que se distribuyen de manera normal, siempre podemos calcular la probabilidad de obtener un rendimiento superior o inferior a un determinado valor. Como uno puede imaginarse, esto tiene implicaciones muy significativas en la formulación de modelos financieros.
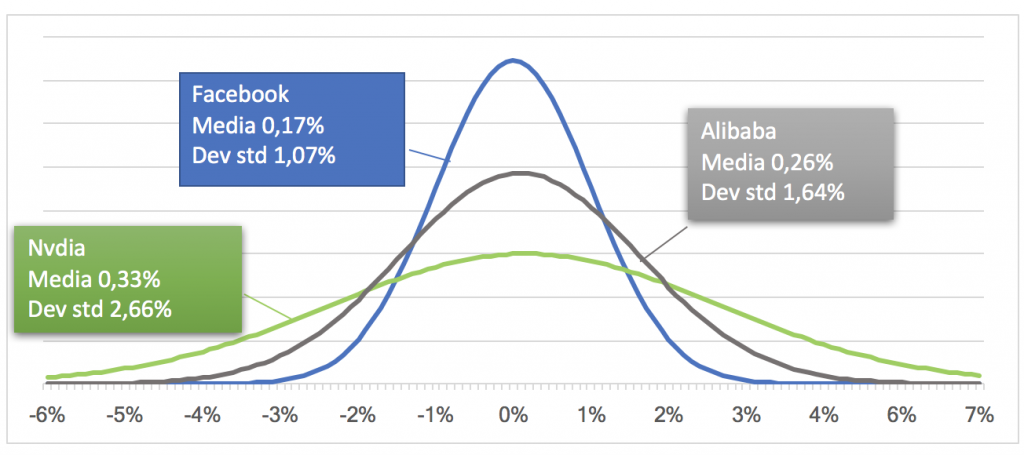
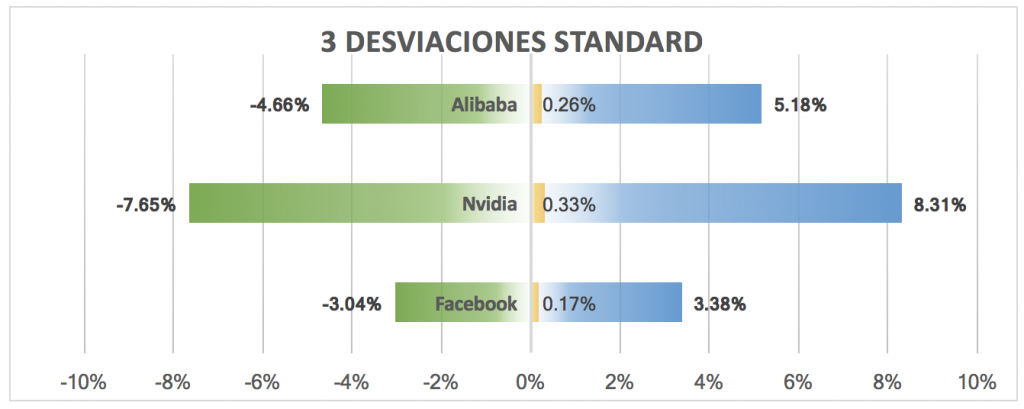
Un alejamiento de la media de 2 o 3 desviaciones estándar toma una dimensión diferente dependiendo de la volatilidad del activo en cuestión. Tomemos como ejemplo la media y la desviación estándar diaria de los retornos registrados en el último año por Facebook, Nvidia y Alibaba.
Un movimiento diario de 3 desviaciones estándar (3 sigma) es equivalente a una desviación de los respectivos promedios de 3.21% para Facebook (-3.04%, 3.38%), 7.98% para Nvidia (-7.65%, 8.31%) y 4.92% para Alibaba (4,66%, 5,18%).
Por lo tanto Nvidia sería la empresa con más expectativa de rentabilidad pero a la vez más riesgo (ya que desviación estándar=volatilidad=riesgo).
¿Los mercados financieros cumplen con estas regularidades estadísticas?
Uno puede preguntarse si los rendimientos efectivos encontrados en la realidad respetan estas reglas.
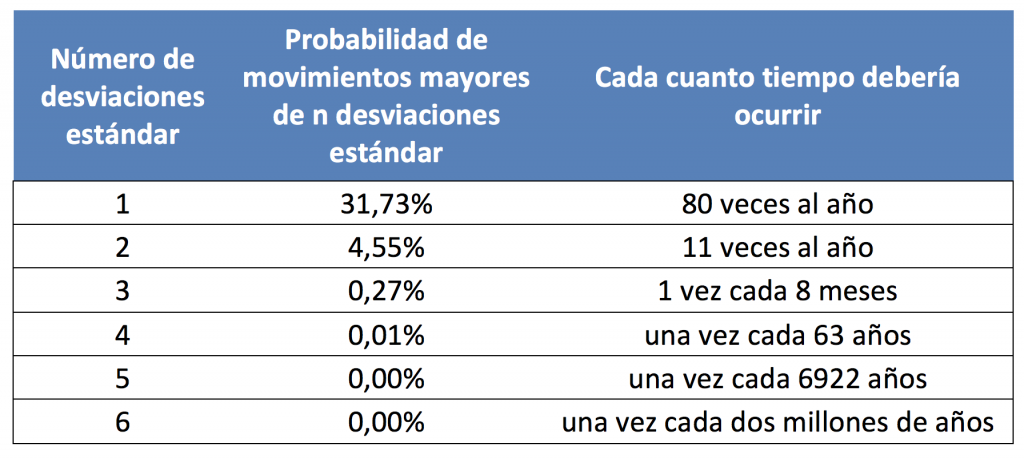
Tratemos de calcular la probabilidad de que los rendimientos diarios de una inversión se desvíen del promedio para un cierto número de desviaciones estándar.
Más allá de las 6 desviaciones estándar, la probabilidad predicha por una distribución normal se vuelve tan remota que el evento es absolutamente improbable.
¿Es realmente así?
A los eventos inesperados se los acostumbra a llamar cisnes negros. El 19 de octubre de 1987, el lunes negro, el índice de S&P cayó un 23% (¡25 desviaciones estándar!). La probabilidad de un evento de desviación estándar de 25 equivale a ganar 21 o 22 veces una lotería de 2,5 millones de euros comprando un billete de un euro (ver este estudio).
Durante la gran crisis de 2007/2008, los eventos siguieron con movimientos que superaron las 20 desviaciones estándar. El día después del referéndum Brexit, la tasa de cambio de la libra esterlina se redujo en 15 desviaciones estándar. Estos fenómenos se consideran prácticamente imposibles si los rendimientos se distribuyen de manera normal.
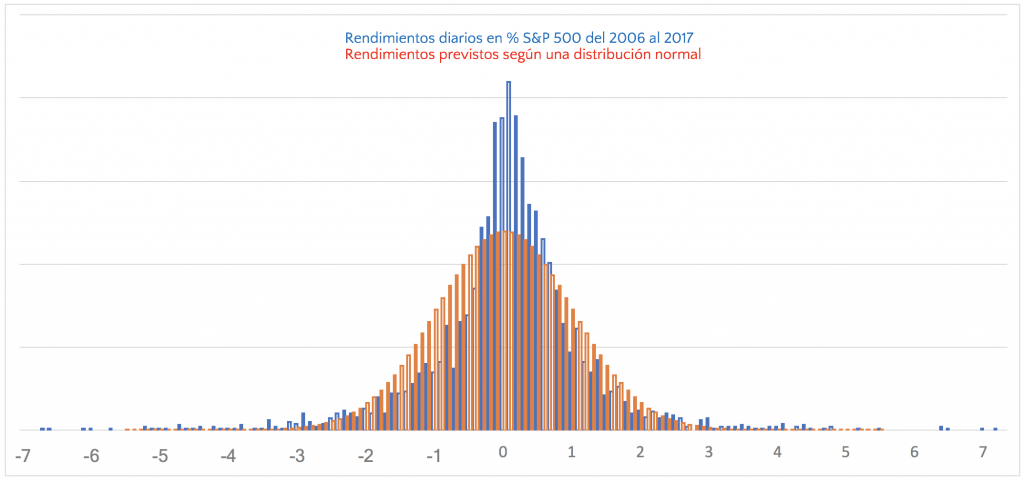
Verificamos empíricamente cómo se distribuyeron los rendimientos diarios de S&P 500 en el período 2006/2015 en comparación con los predichos por una distribución normal con promedio 0 y desviación estándar 1% (para intervalos diarios, el rendimiento esperado puede aproximarse a cero mientras que la desviación estándar diaria de 1950 a la fecha estuvo cerca del 1%).
Desviación estándar, volatilidad y riesgo de las carteras en inbestMe
En inbestMe hay 11 perfiles (del 0 al 10). El número de perfil da una indicación de la exposición a activos de riesgo (renta variable, etc,). De forma indicativa un perfil 5 tendrá aproximadamente un 50% de exposición a renta variable. Cuanto más alto es el perfil más alta es la expectativa de rentabilidad media a largo plazo. Esto tiene su contrapartida en desviación estándar. Como ya hemos indicado en este artículo en el mundo de la inversión la desviación estándar es aceptada generalmente como sinónimo de volatilidad y riesgo. Desafortunadamente en el mundo de la inversión para obtener más rentabilidad hay que aceptar más volatilidad y riesgo. Cuanto más alto sea el perfil más alta es la desviación estándar y por tanto la volatilidad y el riesgo. En la tabla siguiente mostramos las expectativas por perfil de rentabilidad y riesgo de las carteras inbestMe Strategic.
Conclusión
Esperamos que este artículo sirva al lector a entender mejor estos conceptos estadísticos aplicados a las finanzas. Si quieres saber más sobre conceptos te puede interesar saber cómo medir el riesgo de una cartera. Aunque no es imprescindible conocer todos estos cálculos si que es conveniente conocer cual es nuestro perfil de riesgo antes de iniciar una inversión. Si quieres conocer el tuyo clica aquí.