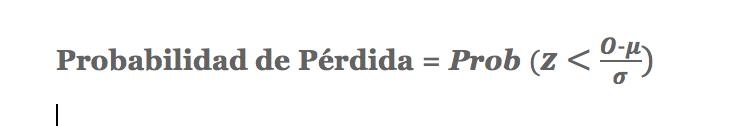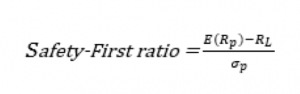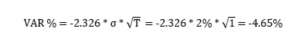¿Cómo se mide el riesgo de una inversión?
La teoría moderna de la cartera ha extendido una noción de riesgo como la volatilidad del rendimiento: más volátil es sinónimo de más arriesgado.
En realidad, el riesgo real para un inversor podría tener diferentes connotaciones, por ejemplo, el de no lograr el objetivo de reservar una cierta cantidad de capital necesario para complementar la pensión, para comprar un apartamento o para enviar a los niños a la universidad; todos estos son riesgos que tienen poco que ver con las fluctuaciones a corto plazo en el valor de la cartera.
En este post, queremos ayudar al inversor a interpretar como evaluar el riesgo de su cartera para poder conseguir sus objetivos financieros.
En particular, un inversor puede querer saber:
- ¿Cuál es la probabilidad de pérdida en su inversión?
- ¿Cuál es la probabilidad de no lograr el rendimiento necesario para alcanzar ciertos objetivos?
- ¿Cuánto es la pérdida máxima que, con una certeza razonable, se puede esperar en un marco de tiempo determinado?
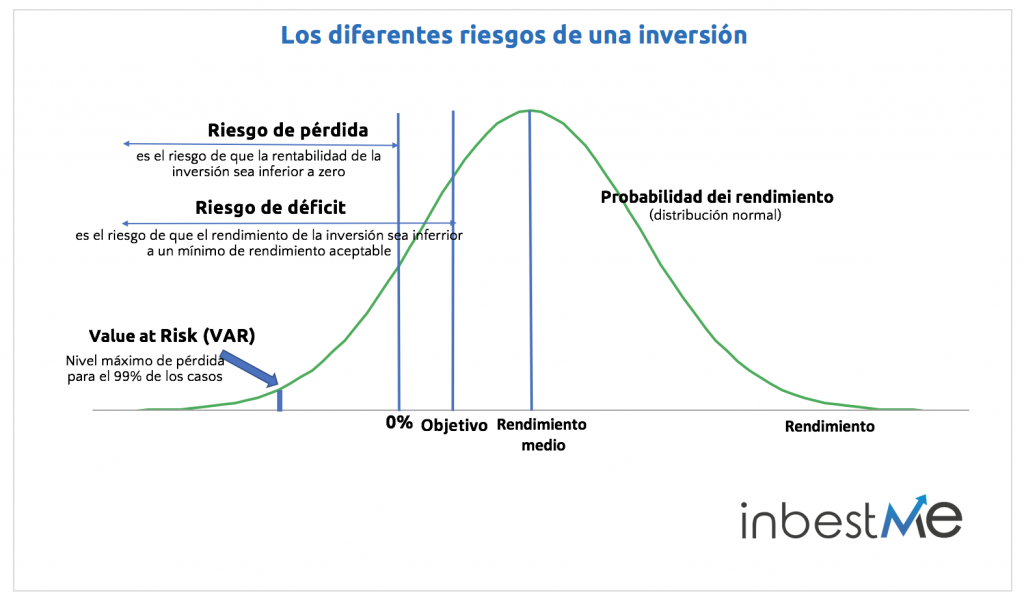
Para responder estas preguntas presentamos 3 conceptos: el riesgo de pérdida, el riesgo de déficit (en relación a un objetivo) y el value at risk (VAR ).
Asumiremos que los rendimientos se distribuyen de manera normal y esto nos permitirá simplificar nuestros comentarios y usar solo dos parámetros: rendimiento promedio y desviación estándar.
El riesgo de pérdida (risk of loss)
Podemos comenzar preguntándonos cuál es la probabilidad de que el rendimiento de una cartera sea menor a cero en un intervalo de tiempo determinado.
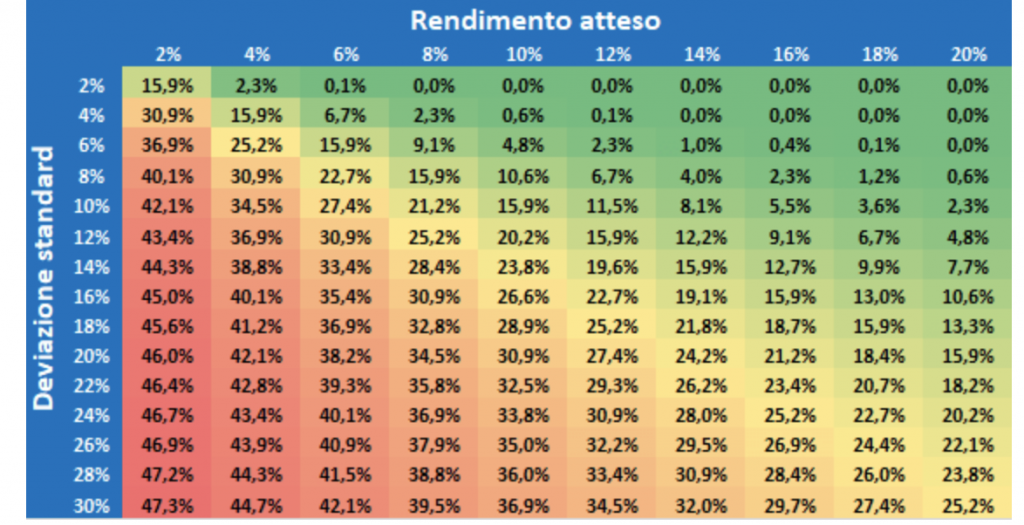
La siguiente tabla muestra la probabilidad de pérdida después de un año para las carteras con diferentes combinaciones de rendimiento esperado y volatilidad. Como se puede esperar, a medida que el rendimiento esperado aumenta y la volatilidad disminuye, la probabilidad de retornos negativos en un año disminuye.
Para calcular esta probabilidad, convertimos la distribución con la media μ y la desviación estándar σ en una distribución estandarizada con media 0 y desviación estándar 1.
La probabilidad de pérdida en un año determinado se calcula como:
donde μ es el rendimiento esperado de la distribución normal y σ es la desviación estándar.
Es posible encontrar este valor en las tablas estadísticas o con la función de Excel DISTRIB.NORM.ST.N (z ; VERDADERO) que devuelve la probabilidad de ocurrencia de valores menores que z.
Por ejemplo, la probabilidad de pérdida en un año para una cartera con un rendimiento esperado del 10% y una volatilidad del 20% es igual a:
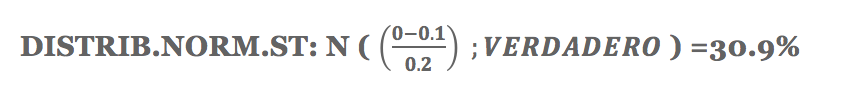
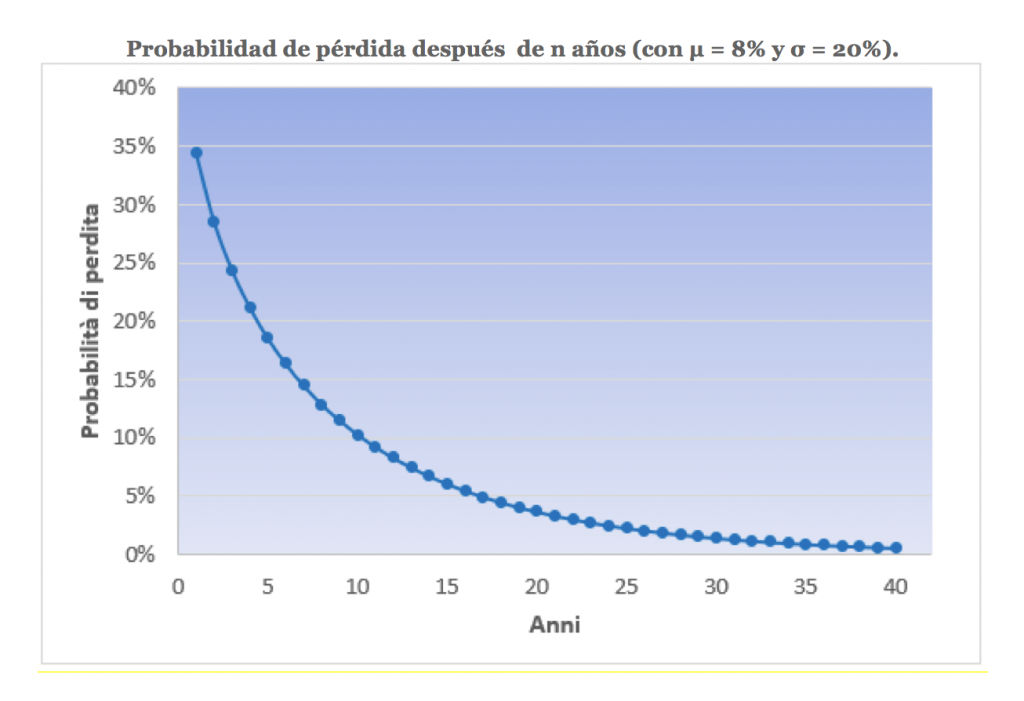
Si la rentabilidad esperada es positiva, la probabilidad de pérdida disminuye a medida que aumenta el número de años en los que la cartera permanece invertida.
Tomemos, por ejemplo, el caso de una cartera con un rendimiento esperado del 8% y una volatilidad del 20%.
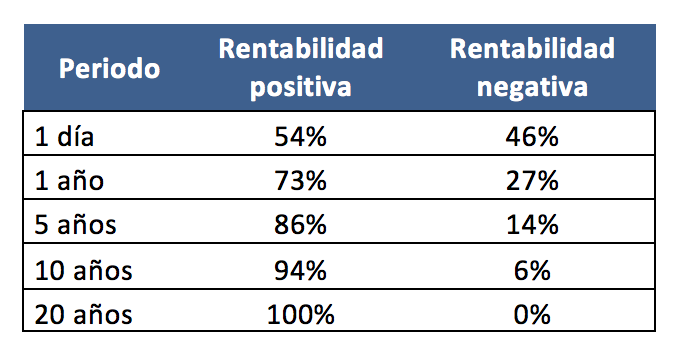
Aquellos que invirtieron durante cualquier período de 20 años en el índice S&P500, de 1926 a 2015, obtuvieron un rentabilidad positiva en todos los casos; aquellos que invirtieron por un período de un año solo lograron un rendimiento positivo en el 73% de los casos.
Rentabilidad del índice S&P 500 durante distintos intervalos (1926/2015).
Por lo tanto el análisis histórico de los rendimientos del S&P500 sugiere que alargar el horizonte temporal es la estrategia más simple y efectiva para disminuir la probabilidad de incurrir en pérdidas.
En inbestMe el riesgo de pérdida medido por la desviación standard es una de las medidas de riesgo que controlamos de nuestras carteras.
Riesgo de déficit (en relación a un objetivo)
El shortfall risk o riesgo de déficit mide el riesgo de que el rendimiento sea inferior a un cierto umbral mínimo aceptable para el inversor.Si una medida de riesgo de volatilidad puede tener poco que ver con las aspiraciones del inversor, el shortfall risk expresa el riesgo concreto de que la inversión no genere el rendimiento mínimo necesario para alcanzar los objetivos del inversor.
Donde r es el rendimiento deseado, μ es el rendimiento esperado, σ es la desviación estándar y T es el número de períodos.
La probabilidad de pérdida es solo un caso especial del riesgo de déficit en el que se ubica r = 0.
Un enfoque utilizado para gestionar el shortfall es el criterio Roy’s Safety-First. El objetivo es seleccionar la cartera que minimice la probabilidad de que el rendimiento caiga por debajo del nivel mínimo aceptable. La cartera que se elegirá es la que tenga la mayor proporción de seguridad primero. Esto se define como:
Donde E (Rp) es la rentabilidad esperada de la cartera, RL es el rendimiento mínimo aceptable y σp es la desviación estándar de la cartera.
Cuanto mayor sea el Safety-First menor será la probabilidad de shortfall. El Safety-First indica en cuántas desviaciones estándar el rendimiento mínimo aceptable dista del rendimiento esperado de la cartera.
Supongamos que tiene que elegir entre dos carteras:
Cartera A con una rentabilidad esperada del 8% y una desviación estándar del 5%;
Cartera B con un rendimiento esperado del 15% y una desviación estándar del 20%. Establecemos el rendimiento mínimo aceptable en 3%.
Entre las dos carteras, se elegirá la que tenga la mayor Safety-First ratio , es decir, la cartera A, cuyo rendimiento esperado dista más, en términos de desviaciones estándar, que el rendimiento mínimo aceptable. Si calculamos la probabilidad de shortfall para la cartera A, obtenemos un 15,9%, mientras que para la cartera B obtenemos un 27,4%.
Cuando el rendimiento mínimo aceptable es la tasa libre de riesgo, el safety first coincide con el Sharpe ratio.
El Value at Risk (VAR)
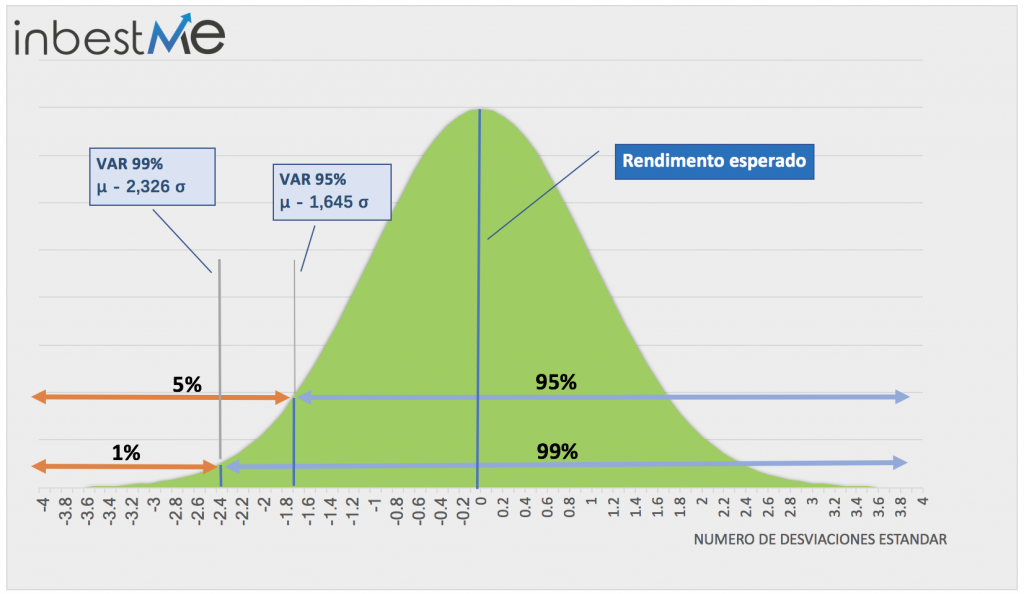
Value at Risk significa la pérdida potencial máxima que una cartera puede sufrir en un período de tiempo determinado con una cierta probabilidad (también llamada nivel de confianza). El nivel de confianza va en general del 95% al 99%.
Decir que el VAR es de 100 mil euros con un nivel de confianza del 99% equivale a decir que en el 99% de los casos la pérdida no excederá los 100 mil euros. En el 1% restante de los casos, la pérdida puede superar los 100 mil euros.
Entonces, el VAR depende de dos parámetros:
- El nivel de confianza Existe una relación directa entre el nivel de confianza y el Var; a medida que aumenta el nivel de confianza, la pérdida potencial aumenta, pero es menos probable. Intuitivamente, si considero una mayor pérdida potencial, aumenta la probabilidad de que no se supere.
- El intervalo de tiempo considerado. El VAR aumenta proporcionalmente a la raíz cuadrada del intervalo de tiempo considerado. Por ejemplo, el VAR de 2 días es igual al VAR de 1 día multiplicado por la raíz cuadrada de 2, por lo que no es el doble del VAR de un día, sino solo el 41.4% mayor.
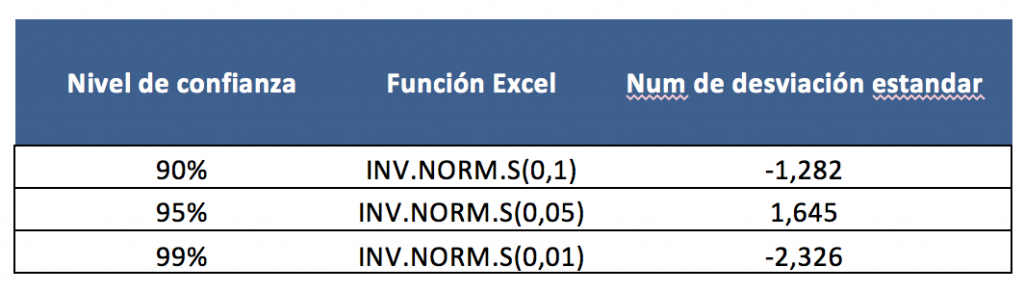
También en este caso, la desviación del promedio se calcula en términos de desviaciones estándar. Si quiero calcular el VAR con una confianza del 99%, debo calcular el número de desviaciones estándar para restar del promedio y dejar solo el 1% de las ganancias a mi izquierda.
Para saber el número de desviaciones estándar, use las tablas estadísticas o la función de excel INV.NORM.S.
Por ejemplo, al restar del promedio de 2.326 desviaciones estándar, obtenemos ese rendimiento que deja a la izquierda solo el 1% de los casos.
Supongamos que queremos calcular el VAR diario de una acción. La desviación estándar diaria es del 2%. Con respecto al rendimiento esperado podemos suponer que, para un intervalo tan corto, es cero.
El porcentaje de VAR para el nivel de confianza del 99% se obtiene como:
Donde T es el número de períodos considerados.
Por lo tanto, esperamos que en el 99% de los casos la pérdida en términos porcentuales sea menor al 4,65%.
Si en vez del VAR en términos porcentuales queremos un VAR en términos monetarios, tenemos que multiplicar el VAR% por el valor de la posición.
Si el valor de la posición es de 1 millón de euros, el% VAR diario se traduce en un VAR en términos absolutos de 46500 euros.
Por lo tanto, en una posición de 1 millón, podemos esperar que, en el 99% de los casos, la pérdida diaria no supere los 46500 €.
El VAR obtenido con esta metodología, utilizando solo la media y la desviación estándar de la distribución, se denomina paramétrico. También se puede obtener una medición del VAR mediante el análisis de datos históricos o con simulaciones de Monte Carlo.
En inbestMe medimos y controlamos periódicamente el VAR de las carteras de nuestros clientes.