Les múltiples cares de la rendibilitat III

En anteriors posts hem pugut veure les diferents formes de calcular la rendibilitat.

En aquest post veurem en la pràctica l’efecte que produeixen diferents situacions en el càlcul de la rendibilitat en funció de les diferents fórmules de càlcul. A través dels exemples, veurem que els fluxos addicionals de diners són els que provoquen la principal distorsió en els càlculs i quina és la millor fórmula per evitar aquesta distorsió.

Rendibilitat lineal en els períodes sense fluxos de caixa addicionals

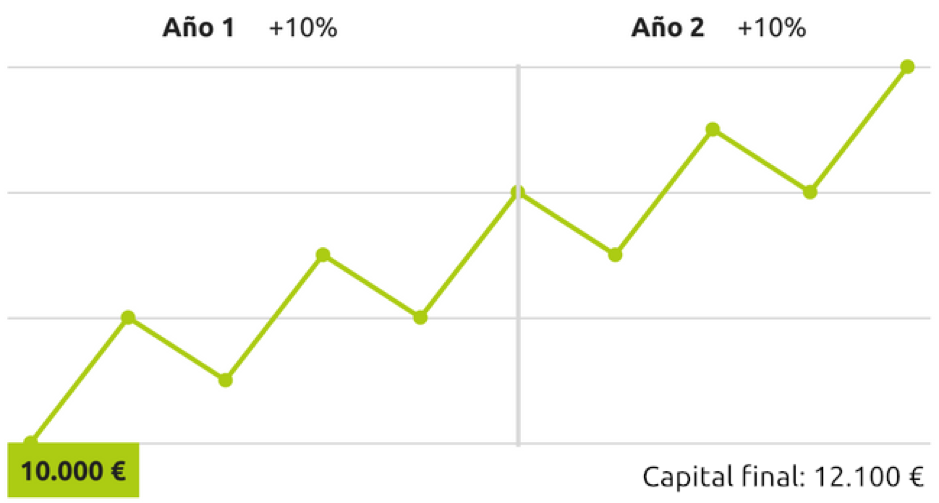
Ja hem vist en altres posts que aquest cas és l’únic que no dóna problemes en els càlculs. És a dir, en totes les fórmules les rendibilitats obtingudes són iguals:

Càlcul simple de la rendibilitat: el 21% (12.100 / 10.000) -1

Rendibilitat ponderada pel temps: 21% ((1 + 0-10) * (1 + 0.10)) – 1

Rendibilitat ponderada pels diners: el 21% 12.100 = (10.000 * (1 + i) ^ 2

i = 10%

(1 + 0.10) ^ 2-1 = el 21%

El que passa és que normalment, la realitat de la vida d’una cartera d’inversió passa per situacions més complexes. Normalment hi ha aportacions o sortides de capital en el temps, i les rendibilitats són irregulars.

Vegem altres casos:

Rendibilitat lineal en els períodes, però amb flux de caixa addicional

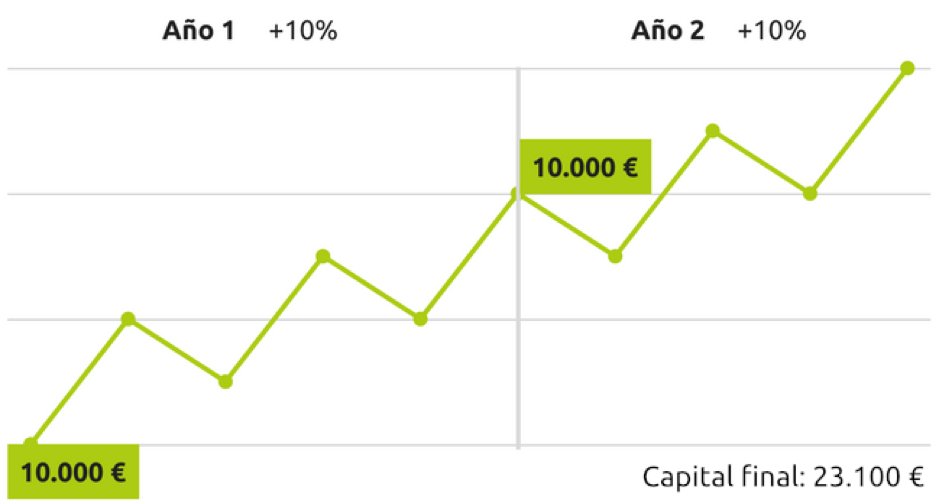
També hem estudiat aquest cas anteriorment. Els càlculs difereixen segons la fórmula utilitzada. Rendibilitat ponderada pel temps o pels diners, donen el mateix resultat.

Càlcul simple de la rendibilitat: 15,5% 23.100 / 21.000-1

Rendibilitat ponderada pel temps: 21% ((1 + 0-10) * (1 + 0.10)) – 1

Rendibilitat ponderada pels diners: el 21% 12.100 = (10.000 * (1 + i) ^ 2) + (10.000 * (1 + i) ^ 1

i = 10%

(1 + 0.10) ^ 2-1 = el 21%

No obstant això, el càlcul de la rendibilitat simple ja ens dona una visió distorsionada.

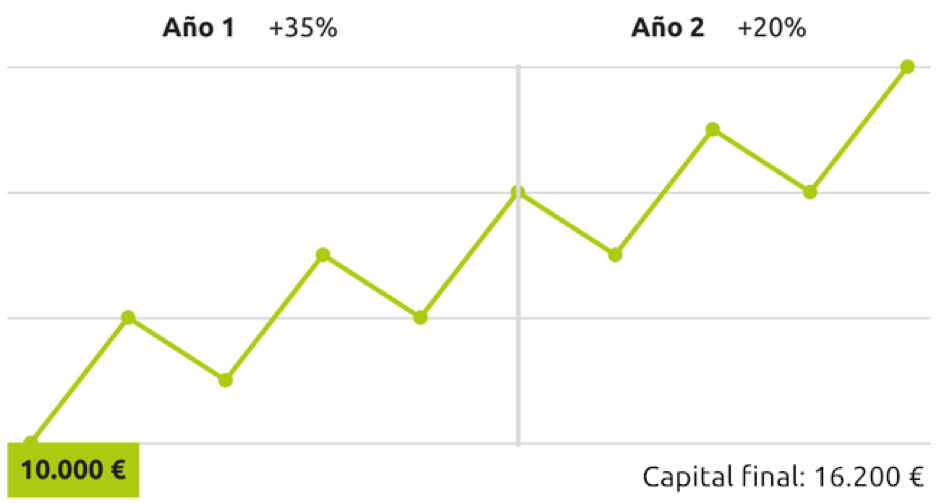
Rendibilitat positiva diferent en els períodes sense fluxos de caixa

Les diferents rendibilitats parcials en els subperíodes no provoquen diferència en el càlcul de la rendibilitat:

Càlcul simple de la rendibilitat: 62% 16.200 / 10.000-1

Rendibilitat ponderada pel temps: 62% ((1 + 0.35) * (1 + 0.20)) – 1

Rendibilitat ponderada pels diners: 62% 16.200 = 10.000 * (1 + i) ^ 2

i = 27.28%

(1 + 0,2728) ^ 2-1 = 62%

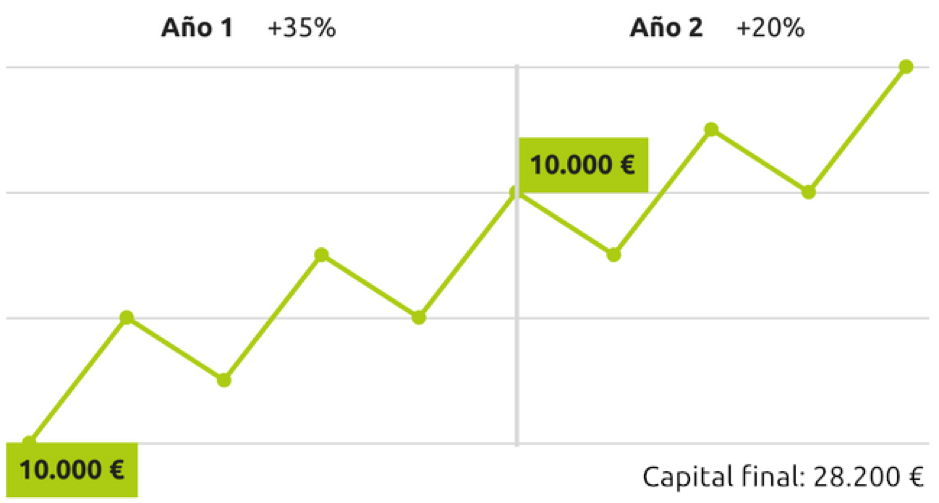
Rendibilitat positiva diferent en els períodes amb flux de caixa

Com veiem en aquest cas, el flux de caixa addicional provoca de nou diferències significatives en el càlcul de rendibilitats:

Càlcul simple de la rendibilitat: 41% (28.200 / 20.000) -1

Rendibilitat ponderada pel temps: 62% ((1 + 0.35) * (1 + 0.20)) – 1

Rendibilitat ponderada pels diners: 56,8% 28.200 = (10.000 * (1 + i) ^ 2) + 10.000 * (1 + i) ^ 1)

i = 25.2%
(1 + 0,252) ^ 2 – 1 = 56.8%

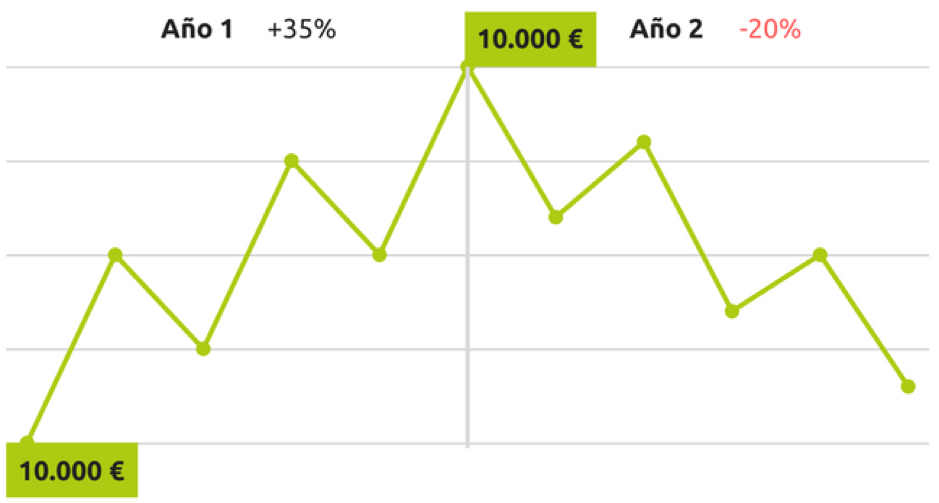
Rendibilitat positiva el primer any, negativa el segon amb flux de caixa

Aquest és possiblement el cas més difícil d’entendre. La sensació per a l’inversor, és d’estar perdent diners, ja que el seu valor final és inferior a la inversió realitzada. En aquest cas el client ha aportat 20,000 €. Això queda reflectit tant en el càlcul de la rendibilitat simple com a la ponderada pels diners. Però no és així en la rendibilitat ponderada pel temps, que és positiva. Pot ser d’ajuda el pensar que la combinació d’un any bo del + 35% amb un any dolent d’un -20%, ha de donar com a resultat una rendibilitat positiva. Una indicació d’això és que la mitjana aritmètica (tot i no ser una mesura vàlida, sí és indicativa) donaria 7,5%, proper al 8%, que ens reflecteix la rendibilitat ponderada pel temps.

Càlcul simple de la rendibilitat: -6% 18.800 / 10.000 -1

Rendibilitat ponderada pel temps: + 8% ((1 + 0.35) * (1 – 0.20)) – 1 = 8.0%

Rendibilitat ponderada pels diners: -7,9% 18.800 = (10.000 * (1 + i) ^ 2) + (10.000 * (1 + i) ^ 1)

i = -4.1%
(1 – 0.041) ^ 2 – 1 = -7.9%

És per aquesta raó que la rendibilitat ponderada pel temps, és la fórmula utilitzada per la indústria financera, ja que és la que reflecteix millor l’impacte real en la rendibilitat de la gestió d’una cartera i permet comparar entre actius. També és el càlcul utilitzat per omissió per InbestMe.

Et recomanem llegir aquests dos articles addicionalment per entendre més sobre aquest tema:

Les múltiples cares de la rendibilitat I

Les múltiples cares de la rendibilitat II

[